Radical of a Lie algebra

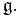
In the mathematical field of Lie theory, the radical of a Lie algebra $\mathfrak{g}$ is the largest solvable ideal of $\mathfrak{g}.$

Definition

Let $k$ be a field and let $\mathfrak{g}$ be a finite-dimensional Lie algebra over $k$ . A maximal solvable ideal, which is called the radical, exists for the following reason.

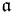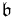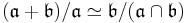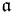Firstly let $\mathfrak{a}$ and $\mathfrak{b}$ be two solvable ideals of $\mathfrak{g}$ . Then $\mathfrak{a}%2B\mathfrak{b}$ is again an ideal of $\mathfrak{g}$ , and it is solvable because it is an extension of $(\mathfrak{a}%2B\mathfrak{b})/\mathfrak{a}\simeq\mathfrak{b}/(\mathfrak{a}\cap\mathfrak{b})$ by $\mathfrak{a}$ . Therefore we may also define the radical of $\mathfrak{g}$ as the sum of all the solvable ideals of $\mathfrak{g}$ , hence the radical of $\mathfrak{g}$ is unique. 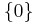Secondly, as $\{0\}$ is always a solvable ideal of $\mathfrak{g}$ , the radical of $\mathfrak{g}$ always exists.

Related concepts

A Lie algebra is semisimple if and only if its radical is $0$ .
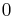A Lie algebra is reductive if and only if its radical equals its center.